Première partie - Étalonnage du dispositif
Méthode : Étalonner le dispositif
Le dispositif est étalonné à l'aide du spectre du mercure dont on connaît les longueurs d'ondes des raies principales avec une précision satisfaisante. Lors de la séance de travaux pratiques quatre raies du mercure ont été utilisées.
Violet | Indigo | Vert | Jaune/orange |
|---|---|---|---|
404,7 nm | 435,8 nm | 546,1 nm | 577,5 nm |
Sur l'écran, le spectre est symétrique par rapport à l'image de la fente source. On mesure la distance d séparant chaque raie de l'image de la fente source avec la plus grande précision possible, en étalant au maximum le spectre sur l'écran.
Complément : Incertitude sur la mesure de la distance d
On mesure la distance d avec un réglet dont la précision est \(p=1\ \mathrm{mm}=0{,}1\ \mathrm{cm}\).
L'incertitude correspond à une double mesure : origine et position de la raie. Dans ce cas de figure on peut montrer que l'incertitude type u(d) sur la mesure de d se calcule par la relation : \(u(d)=\dfrac{p}{\sqrt 6}\).
Cette incertitude est la même pour toutes les mesures de d et vaut : \(u(d)\simeq 0{,}04\ \mathrm{cm}\), arrondie à un seul chiffre significatif.
Exemple : Mesures obtenues par l'enseignant
\(\lambda\ \mathrm{(nm)}\) | 404,7 | 435,8 | 546,1 | 577,5 |
|---|---|---|---|---|
\(d\ \mathrm{(cm)}\) | 7,95 | 8,55 | 10,85 | 11,50 |
\(u(d)\ \mathrm{(cm)}\) | 0,04 | 0,04 | 0,04 | 0,04 |
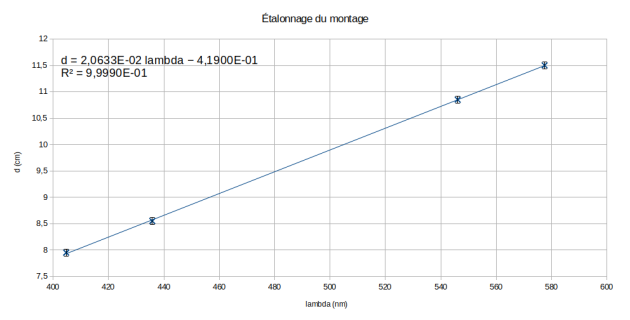
On obtient la droite d'étalonnage ci-dessous :
Vous pouvez télécharger le fichier au format Libre Office Calc en cliquant ci-dessous.
Les barres d'incertitudes sont de faible amplitude et permettent de valider le modèle. Dans la suite on négligera les incertitudes sur le coefficient directeur et l'ordonnée à l'origine de la droite.
On a obtenu la relation mathématique suivante : \(d=a×\lambda+b\).
Avec :
\(a=2{,}0633\times10^{−2}\ \mathrm{cm\cdot nm^{−1}}\)
\(b=−0{,}4190\ \mathrm{cm}\)
La longueur d'onde \(\lambda\) se calcule donc à partir de la distance d par la relation : \(\lambda=\dfrac{d-b}{a}\).