Exercice : Détermination de la transition énergétique à l'origine de la raie jaune du sodium
Question
On donne ci-contre quelques niveaux d'énergie de l'atome de sodium.
Identifiez la transition énergétique à l'origine de la raie jaune observée et dont la longueur d'onde a été calculée à la question précédente.
Solution
Le photon émis à la longueur d'onde \(\lambda_{Na}=587\ \mathrm{nm}\) avec une incertitude type de 2 nm possède une énergie strictement égale à un écart d'énergie entre deux niveaux de l'atome.
La réponse s'effectue en deux temps :
Calcul de l'énergie du photon émis.
Identification de deux niveaux d'énergie séparés de cette valeur.
On calcule l'énergie du photon à l'aide de la relation de Planck-Einstein :
\(E_{photon}=h \times \dfrac{c}{\lambda_{Na}}\)
Application numérique :
\(E_{photon}=\dfrac{6{,}63 \times 10^{-34}\times3{,}00\times 10^8}{587\times 10^{-9}}\simeq 3{,}39\times 10^{-19}\ \mathrm J\)
Soit en eV :
\(E_{photon}=\dfrac{3{,}39\times 10^{-19}}{1{,}602\times 10^{-19}}\simeq 2{,}12\ \mathrm{eV}\)
L'énergie du photon émis correspond exactement (à l'incertitude près) à l'écart énergétique \(\Delta E\) entre les deux niveaux impliqués.
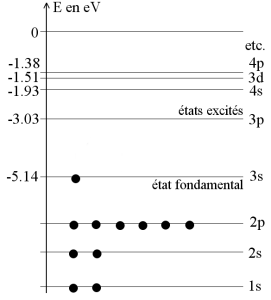
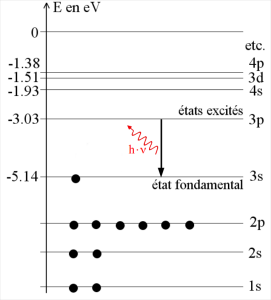
Sur le diagramme des niveaux d'énergie du sodium, on constate que \(\Delta E=E_{3p}-E_{3s}=2{,}11\ \mathrm{eV}\). Aucun autre écart énergétique ne conduit à une valeur correspondant à l'énergie du photon émis.
La raie jaune du sodium est donc émise par des atomes de sodium passant de l'état excité 3p à l'état fondamental 3s.
Cette transition énergétique peut se schématiser comme sur la figure ci-contre.
Calcul complémentaire - prise en compte de l'incertitude sur l'énergie du photon
L'incertitude sur la longueur d'onde se propage à l'énergie du photon. Il peut être nécessaire de déterminer l'incertitude élargie sur l'énergie du photon pour s'assurer de l'unicité du \(\Delta E\) associé. Si cette incertitude est trop importante, plusieurs transitions énergétiques peuvent correspondre et on ne peut pas trancher précisément.
On peut montrer que l'incertitude type sur l'énergie est donnée par la relation :
\(u(E)=\dfrac{h \cdot c}{\lambda^2}\cdot{u(\lambda)}\)
Soit numériquement :
\(u(E)=\dfrac{6{,}63\times 10^{-34}\times 3\times10^8}{\left(587\times 10^{-9}\right)^2}\times 2{,}0\times 10^{-9}\simeq1{,}15\times 10^{-21}\ \mathrm J\), soit en eV \(u(E)\simeq7\times 10^{-3}\ \mathrm{eV}\)
L'incertitude type sur la valeur de l'énergie du photon est faible, donc il n'y a pas d’ambiguïté sur la transition énergétique concernée. Seule la transition 3p → 3s est possible.