Modélisation mathématique : loi de Snell-Descartes
Étude expérimentale
Fiche d'activité expérimentale
Vous pouvez télécharger ci-dessous la fiche d'activité distribuée en classe.
Exemple : Exemples de résultats obtenus
Vous pouvez télécharger ci-dessous un exemple de mesures obtenues par un des groupes de la classe ainsi que quelques feuilles de calculs regroupées dans un fichier compressé.
Téléchargez ci-dessous une feuille de calcul avec les résultats d'un groupe.
Vous pouvez accéder aux fichiers de mesures partagés par quelques groupes en accédant au dossier suivant :
https://nuage03.apps.education.fr/index.php/s/ZeMpp8YZ4DM4S5S
Vérification de l'affirmation de Kepler
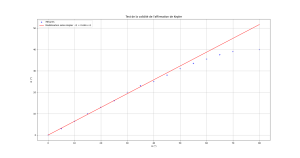
Les mesures des angles d'incidence et de réfraction montrent effectivement une relation de proportionnalité entre i1 et i2 tant que \(i_1 \leq 40^\circ\).
Dans le cas présent, la relation de proportionnalité dans la gamme où la modélisation de Kepler est valide est :
\(i_2=0{,}646\times i_1\)
Vérification de l'affirmation de Snell-Descartes
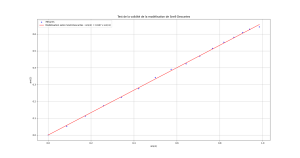
La représentation graphique ci-contre montre que la proportionnalité entre \(\sin i_1\) et \(\sin i_2\) est vérifiée sur toute la gamme de variation de l'angle i1.
La relation de proportionnalité obtenue en calculant le coefficient directeur de la droite est :
\(\sin i_2=0{,}667\times \sin i_1\)
Méthode : Lien entre le coefficient de proportionnalité et les indices de réfraction des milieux de propagation
Dans le cas du passage d'un rayon lumineux de l'air dans le plexiglas, on peut montrer que la relation de proportionnalité entre les sinus s'écrit en faisant intervenir les indices de réfraction de l'air et du plexiglas :
\(\sin i_2=\dfrac{n_{air}}{n_{plexi}}\times \sin i_1\)
Avec les valeurs données dans la fiche de TP, on attends comme résultat pour le coefficient de proportionnalité :
\(\dfrac{n_{air}}{n_{plexi}}=\dfrac{1{,}00}{1{,}50}\simeq0{,}667\)
Dans l'exemple choisi, les deux valeurs sont cohérentes et égales pour un résultat arrondi à 3 chiffres significatifs.
Complément : Fiche TP annotée
Vous pouvez télécharger ci-dessous la fiche de TP avec les annotations prises lors de la séances et notamment le dernier calcul plus détaillé.
Bilan
Relation mathématique
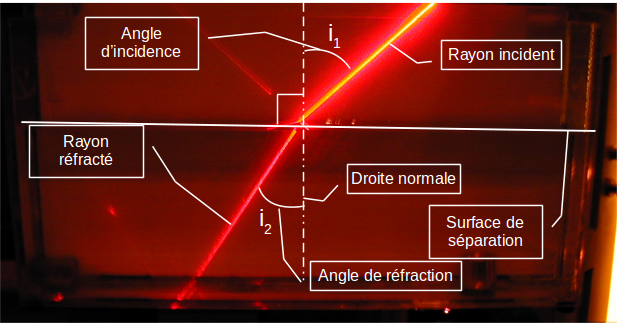
On a montré par des mesures d'angles suivies d'une analyse sur tableur que les angles d'incidence et de réfraction sont liés par une relation appelée loi de Snell-Descartes.
Elle stipule que les sinus des angles d'incidence et de réfraction sont proportionnels.
Pour un rayon lumineux passant d'un milieu d'indice n1 à un milieu d'indice n2, on écrit cette relation de proportionnalité de la façon suivante :
Méthode : Application - Détermination de l'indice de réfraction d'un milieu transparent
Un réfractomètre est un petit appareil permettant de mesurer l'indice de réfraction d'un milieu.
Cette détermination se base sur la mesure de l'angle d'incidence i1 et l'angle de réfraction i2. On connaît par ailleurs un des deux indices de réfraction intervenant dans la relation de Snell-Descartes.
On obtient donc l'indice de réfraction inconnu par \(n_2=n_1 \times \dfrac{sin\ i_1}{sin\ i_2}\).
Par exemple, si pour un angle d'incidence \(i_1 = 30{,}0°\), on mesure \(i_2 =27{,}0°\) et que le milieu n°1 est de l'air d'indice \(n_1=1{,}00\) alors on a \(n_2=\dfrac{sin\ 30{,}0°}{sin\ 27{,}0°}\simeq 1{,}10\).

Méthode : Application - Prévision de l'angle de réfraction
Si on connaît les deux milieux de propagation, notamment leurs indices de réfraction n1 et n2, il est possible de prévoir la trajectoire du rayon réfracté en calculant l'angle de réfraction i2.
On détermine dans un premier temps \(sin\ i_2\) par la relation \(sin\ i_2=\dfrac{n_1}{n_2} \times sin\ i_1\).
On utilise la calculatrice pour ensuite déterminer la valeur de l'angle i2 à partir de la valeur du sinus.
Exemple numérique :
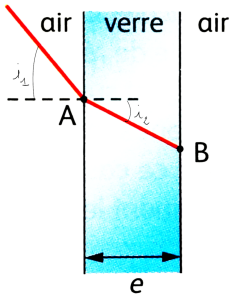
Dans l'exemple ci-contre, le milieu n°1 est de l'air d'indice \(n_1=1{,}00\) et le milieu n°2 du verre d'indice \(n_2=1{,}50\). Supposons que l'angle d'incidence est \(i_1=30{,}0°\).
On commence par calculer le sinus de l'angle de réfraction :
\(sin\ i_2=\dfrac{1}{1{,}50} \times sin\ 30{,}0° \simeq 0{,}333\)
On obtient maintenant l'angle i2 correspondant : \(i_2=arcsin\ 0{,}333 \simeq 19{,}5°\).