Exercice : Application à l'analyse quantitative d'une solution - Une solution d'acide nitrique
Question
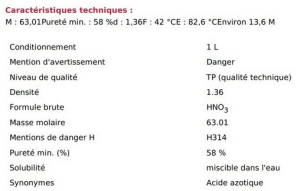
On donne ci-contre les caractéristiques d'une solution d'acide nitrique dite à 58 %. Cette indication est la pourcentage massique de la solution en \(HNO_3\).
Relevez les indications que vous savez interpréter sur cette étiquette.
Exploitez ces indications pour calculer la concentration massique de la solution en \(HNO_3\).
Comment comprenez-vous l'indication de masse molaire sachant qu'elle s'exprime en \(\mathrm{g \cdot mol^{-1}}\) ?
Exploitez cette indication pour calculer la quantité de matière de \(HNO_3\) dans 1 litre de solution.
On définit la concentration molaire ou concentration en quantité de matière d'une espèce chimique en solution comme le rapport du nombre de moles n de l'espèce chimique sur le volume V de la solution.
Quelle est la concentration molaire en \(HNO_3\) de la solution ?
Solution
On reconnaît sur l'étiquette :
le pourcentage massique en acide nitrique, aussi appelé pureté sur l'étiquette : \(p\left(HNO_3\right)=58\% = 0{,}58\) ;
volume de la solution : \(V=1{,}0\ \mathrm{L}\) ;
densité, dont on déduit la masse volumique de la solution : \(\rho = 1{,}36\ \mathrm{g \cdot mL^{-1}}=1360\ \mathrm{g\cdot L^{-1}}\)
On obtient la concentration massique en calculant dans un premier temps la masse \(m\left(HNO_3\right)\) d'acide nitrique présent dans la solution.
D'après les données de l'étiquette, un litre de solution pèse 1360 grammes. 58% de cette masse est due à l'espèce chimique \(HNO_3\).
Donc : \(m\left(HNO_3\right)=0{,}58 \times 1360 \simeq788{,}8\ \mathrm g\)
\(t\left(HNO_3\right)=\dfrac{m\left(HNO_3\right)}{V}=788{,}8\ \mathrm{g \cdot L^{-1}}\), avec \(V=1{,}0\ \mathrm L\).
D'après l'unité utilisée pour exprimer la masse molaire, on peut en déduire que cette valeur correspond à la masse d'une mole de l'espèce chimique considérée. D'après cette indication, une mole de molécules \(HNO_3\) a une masse égale à \(63{,}01\ \mathrm g\).
La quantité de matière \(n \left(HNO_3\right)\) se calcule à l'aide de la masse molaire et de la masse dissoute en solution par \(n\left(HNO_3\right)=\dfrac{m\left(HNO_3\right)}{M\left(HNO_3\right)}\).
Soit numériquement : \(n\left(HNO_3\right)=\dfrac{788{,}8}{63{,}01}\simeq12{,}5\ \mathrm {mol}\)
D'après l'énoncé de la question, la concentration molaire, notée c, s'exprime par : \(c=\dfrac{n}{V}\).
Dans notre cas de figure, le volume est égal à 1 litre, donc : \(c\left(HNO_3\right)\simeq 12{,}5\ \mathrm{mol \cdot L^{-1}}\)