Mise en œuvre du protocole et exploitation des mesures
Position du problème
Le protocole est basé sur l'étude du fonctionnement d'une DEL (Diode Électroluminescente) et sur la mise en relation de son comportement électrique avec la nature de la lumière émise.
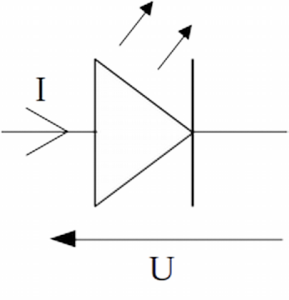
Ci-contre le schéma de la DEL avec l'intensité et la tension. Du point de vue du comportement électrique, on retient les éléments suivants :
Le courant électrique ne peut circuler que dans le sens indiqué par la flèche d'intensité.
La diode est passante que si la tension appliquée à ses bornes dépasse une valeur seuil, notée Useuil : si \(U>U_{seuil}\), alors \(I>0\), sinon l'intensité I est nulle.
Hypothèse de départ
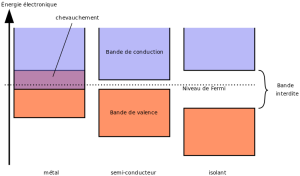
Le fonctionnement d'un semi-conducteur peut s'interpréter à l'aide de la notion de bandes d'énergie occupées par les électrons.
La bande d'énergie la plus basse est la bande de valence. Les électrons occupant des énergies dans cette bande sont plus fortement liés au solide et ne participent pas à la conduction du courant électrique.
La bande de conduction quant à elle occupe des énergies plus élevées. Il faut donc communiquer de l'énergie aux électrons pour les faire passer de la bande de valence à la bande de conduction pour que du courant électrique circule.
Dans un semi-conducteur, la bande interdite est suffisamment faible pour que ce passage soit possible.
Dans le cas d'une DEL, on montre que l'énergie a fournir à un électron pour le faire passer de la bande de valence à la bande de conduction s'exprime en fonction de la tension de seuil : \(\Delta E=e \times U_{seuil}\), où e est la charge élémentaire \(\left(e \simeq 1{,}602 \times 10^{-19}\ \mathrm C \right)\).
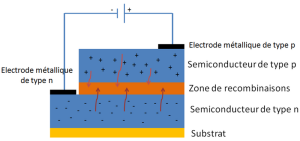
En ce qui concerne l'émission de lumière par la DEL, celle-ci a lieu lorsque des électrons de la bande de conduction se recombinent avec des "trous" dans la zone de recombinaison. Lorsque la DEL conduit le courant électrique, électrons et trous migrent en sens inverses dans le composant. En se recombinant, l'électron cède l'énergie qu'il possédait pour retomber dans la bande de conduction en émettant un photon de fréquence \(\mathbf{\nu}\), donc d'énergie \(E_{photon}=h \cdot \nu\).
On considère dans la suite que l'énergie emportée par le photon est égale à l'énergie qu'il a fallu communiquer à l'électron pour le faire passer de la bande de valence à la bande de conduction.
On a donc la relation suivante : \(e \times U_{seuil}=h \times \nu\), soit \(U_{seuil}=\dfrac{h}{e} \times \nu\).
Principe de la mesure
La détermination de la constante de Planck h passe par :
La mesure de la tension de seuil de la DEL après avoir tracé sa caractéristique.
La mesure de la longueur d'onde de la lumière émise.
La détermination du coefficient directeur de la droite représentant les variations de \(U_{seuil}\) en fonction de la fréquence \(\nu\).
Méthode : Détermination de la tension de seuil de la DEL
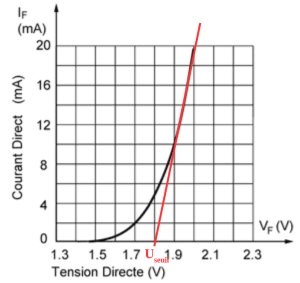
La tension de seuil se détermine comme indiqué sur la figure ci-contre.
Par ailleurs, la vidéo ci-dessous reprend la procédure utilisée avec la logiciel LATIS PRO pour tracer la caractéristique de la DEL et déterminer la valeur de la tension de seuil.
Méthode : Détermination de la fréquence du photon émis
À l'aide de l'équipement Spectro Vio, on obtient le spectre d'émission de chacune des DEL.
On repère la longueur d'onde du pic démission \(\lambda_{max}\), ce qui permet ensuite de déterminer la fréquence du photon par la relation \(\nu=\dfrac{c}{\lambda_{max}}\).
Par exemple, sur la figure ci-contre \(\lambda_{max}=567\ \mathrm{nm}\). On a donc \(\nu=\dfrac{3,00 \times 10^8}{567 \times 10^{-9}} \simeq 5{,}29 \times 10^{14}\ \mathrm{Hz}\).
Bilan des mesures
Les feuilles de calcul téléchargeables ci-dessous reprennent des mesures réalisées par l'enseignant et la mesure issue de la mise en commun lors de la séance de TP.
Vous pouvez télécharger le bilan des mesures réalisées par l'ensemble du groupe ci-dessous.
La modélisation par une droite passant par l'origine permet de déterminer le coefficient \(\dfrac{h}{e}\).
On peut donc finalement obtenir la valeur de la constante de Planck h en utilisant la valeur \(e=1{,}602 \times 10^{-19} \ \mathrm C\).
Exploitation des mesures du groupe
La mise en commun de mesures issues de plusieurs binômes permet un échantillon statistique plus large.
Pour rappel, deux points de mesure réalisés avec des DEL à haute luminosité ont été éliminés, car les valeurs des tensions de seuil étaient clairement incohérentes avec l'hypothèse de travail posée dans l'activité.
La modélisation donne pour valeur numérique du coefficient directeur \(3{,}946\times 10^{-15}\ \mathrm{SI}\).
Donc \(\dfrac{h}{e}=3{,}946\times 10^{-15}\ \mathrm{SI}\), soit numériquement :
\(h=3{,}946\times 10^{-15} \times 1{,}602\times 10^ {-19}\simeq 6{,}32\times 10^{-34}\ \mathrm{J \cdot s}\)
On peut déterminer l'écart relatif e entre la valeur théorique hth et la valeur déterminée expérimentalement hexpe.
\(e=\dfrac{|h_{expe}-h_{th}|}{h_{th}}\times 100\)
\(e=\dfrac{|6{,}32\times10^{-34}-6{,}63\times 10^{-34}|}{6{,}63\times 10^{-34}}\times 100 \simeq 4{,}6 \%\)