Activité expérimentale - Analyse d'un antiseptique - Loi de Beer-Lambert
Fiche d'activité élève
Vous pouvez récupérer ci-dessous la fiche d'activité distribuée.
Colorimètre utilisé
L'appareil utilisé n'est pas à proprement parler un spectrophotomètre. Il ne permet pas de balayer l'ensemble des longueurs d'onde du spectre visible. Seules quelques longueurs d'onde de travail peuvent être sélectionnées à l'aide de filtres colorés.
Pour effectuer une mesure d'absorbance :
Mettre l'appareil sous tension.
Vérifier que l'appareil est en mode Absorbance (Abs sur l'afficheur). Si ça n'est pas le cas, presser le bouton (1).
Sélectionner la longueur d'onde de travail à l'aide de la molette latérale (choisir la plus proche de la position du pic d'absorption repéré sur le spectre).
Il faut "faire le blanc", c'est-à-dire indiquer à l'appareil la référence pour la valeur zéro de l'absorbance. Placer une cuve contenant le solvant utilisé, le plus souvent de l'eau distillée, dans le colorimètre et presser la touche R (2).
Placer la cuve contenant la solution dont on veut mesurer l'absorbance dans le colorimètre et presser la touche T (4).
L'absorbance s'affiche avec deux décimales, c'est une précision satisfaisante si la solution n'est pas trop diluée.
Méthode : Établissement de la loi de Beer-Lambert
On souhaite connaître la concentration de la solution de Dakin à partir d'une mesure d'absorbance.
Il faut donc connaître la relation entre l'absorbance A et la concentration C en ions permanganate. Cette relation constitue la loi de Beer-Lambert.
Dans un premier temps, on déterminer la longueur d'onde de travail en repérant la position du pic d'absorbance sur le spectre d'absorption des ions permanganate.
Sur le spectre ci-contre, on lit la valeur correspondant au pic \(\lambda_{max} \simeq 527\ \mathrm{nm}\).
On règle le colorimètre sur la longueur d'onde la plus proche de \(\lambda_{max}\), soit 520 nm. Cela correspond à l'utilisation d'un filtre vert.
Afin de réaliser plusieurs mesures d’absorbance à des concentrations différentes, on réalise six solutions aqueuses de permanganate de potassium par dilution d'une solution mère.
Les absorbances et concentrations sont consignées dans le tableau ci-dessous (exemple de mesures obtenues dans un précédent TP).
C\(\mathrm{\left( mol \cdot L^{-1} \right)}\) | \(1{,}00 \times 10^{-4}\) | \(7{,}00 \times 10^{-5}\) | \(5{,}00 \times 10^{-5}\) | \(3{,}00 \times 10^{-5}\) | \(2{,}00 \times 10^{-5}\) | \(1{,}00 \times 10^{-5}\) |
|---|---|---|---|---|---|---|
A | 0,21 | 0,15 | 0,11 | 0,07 | 0,04 | 0,02 |
Ces mesures sont exploitées dans un Notebook complet et corrigé disponible dans Capytale avec le code d'accès suivant : 0749-227023.
On obtient la représentation graphique ci-dessous, avec sa modélisation.
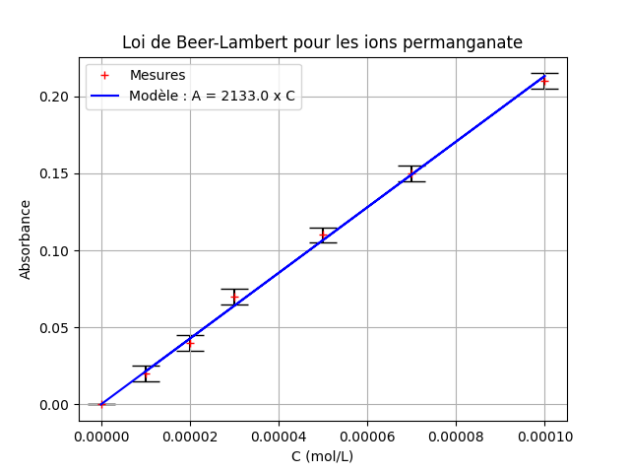
Il apparaît que l'absorbance est proportionnelle à la concentration. Le modèle choisi est en accord satisfaisant avec les points expérimentaux.
Le programme en Python donne la valeur du coefficient de proportionnalité entre l'absorbance A et la concentration en ions permanganate et l'incertitude type sur cette valeur :
\(k=2133\ \mathrm{L \cdot mol^{-1}}\) ;
\(u \left(k \right)\simeq 36{,}5\ \mathrm{L \cdot mol^{-1}}\).
L'incertitude type s'arrondit à un seul chiffre significatif : \(u \left(k \right)=40\ \mathrm{L \cdot mol^{-1}}\). On accorde la précision sur k à celle de l'incertitude type, donc :
\(\mathbf{A=k \times C_{MnO_4 ^{-}}}\), avec \(k=2130\ \mathrm{L \cdot mol^{-1}}\)
La modélisation donne une incertitude type sur le coefficient k \(u \left(k \right)=40\ \mathrm{L \cdot mol^{-1}}\).
Cette relation de proportionnalité constitue la loi de Beer-Lambert pour les ions permanganate à la longueur d'onde de 525 nm.
Méthode : Exploitation pour déterminer la concentration de la solution de Dakin (à partir d'un exemple de mesure)
La connaissance de la loi de Beer-Lambert permet une détermination quasi-immédiate de la concentration de la solution de Dakin en ions permanganate.
On mesure l'absorbance de la solution de Dakin, dans les mêmes conditions que pour les solutions de permanganate de potassium : \(\mathbf{A_{Dakin}=0{,}13}\).
On a donc : \(C_{Dakin}^\text{Mesurée}=\dfrac{A_{Dakin}}{2133}\).
Soit \(C_{Dakin}^\text{Mesurée}=\dfrac{0{,}13}{2133} \simeq 6{,}103 \times 10^{-5}\ \mathrm{mol \cdot L^{-1}}\).
Concentration en permanganate de la solution de Dakin annoncée par le fabricant
Le fabricant indique la concentration massique en permanganate de potassium : \(\mathbf{t=0{,}01\ g \cdot L^{-1}}\).
La masse molaire du permanganate de potassium KMnO_4 est \(M_{KMnO_4}=158{,}0\ \mathrm{g \cdot mol^{-1}}\).
On en déduit la concentration massique annoncée par le fabricant : \(C_{KMnO_4} ^{flacon}=\dfrac{t}{M_{KMnO_4}}\).
Numériquement : \(C_{KMnO_4} ^{flacon}=\dfrac{0,01}{158{,}0} \simeq 6{,}33 \times 10^{-5}\ \mathrm{mol \cdot L^{-1}}\).
Méthode : Écart relatif entre la valeur expérimentale et la valeur théorique
L'écart relatif entre la valeur mesurée et la valeur théorique permet d'estimer la précision de la mesure faute d'un calcul d'incertitude plus complet.
\(e=\dfrac{\left| C_{MnO_4}^{flacon} - C_{Dakin}^{Mesurée} \right|}{C_{MnO_4}^{flacon}} \times 100\).
Application numérique : \(e=\dfrac{\left| 6{,}33 \times 10^{-5} - 6{,}1 \times 10^{-5}\right|}{6{,}33 \times 10^{-5}} \times 100 \simeq 3{,}6\%\).
La valeur mesurée est d'une précision satisfaisante si on retient comme critère le seuil de 5%. Il faut noter que les absorbances ne sont mesurées qu'avec deux décimales. Pour les solutions les moins concentrées, cela limite notablement la précision de la mesure.
Complément : Détermination de l'incertitude type sur la concentration mesurée
La concentration se déduit de la mesure de l'absorbance par : \(C=\dfrac{A}{k}\).
L'incertitude sur la concentration provient de :
l'incertitude sur la mesure de l'absorbance \(u(A)\), estimée en prenant en compte la résolution de l'affichage au centième d'unité ;
l'incertitude sur le coefficient k, \(u(k)\), fournie par la modélisation.
Pour l'absorbance, le colorimètre utilisé affiche la valeur au centième près, donc on peut considérer que la valeur de l'absorbance est à priori comprise dans l'intervalle \(\left[A_{mesure}-0{,}005 ;A_{mesure}+0{,}005 \right]\).
Dans ce cas, on calcule \(u(A)\) par \(u(A)=\dfrac{0{,}005}{\sqrt 3}\simeq 2{,}887\times10^{-3}\)
On peut montrer que les deux incertitudes se combinent pour obtenir l'incertitude relative sur la concentration de la façon suivante :
\(\dfrac{u(C)}{C}=\sqrt{\left(\dfrac{u(A)}{A} \right)^2+\left(\dfrac{u(k)}{k} \right)^2}\)
Numériquement, en prenant des valeurs non arrondies pour les incertitudes types, on obtient :
\(\dfrac{u(C)}{C} \simeq 2{,}50 \times 10^{-2}\)
Donc :
\(u(C)\simeq1{,}53 \times 10^{-6}\ \mathrm{mol\cdot L^{-1}}\)
Arrondi à un seul chiffre significatif, on a : \(u(C) = 2 \times 10^{-6}\ \mathrm{mol\cdot L^{-1}}\)
On écrira donc le résultat de la mesure de la concentration en permanganate avec le nombre de chiffres significatifs cohérent avec la valeur de l'incertitude type :
\(C_{KMnO_4}=6{,}1 \times 10^{-5}\ \mathrm{mol \cdot L^{-1}}\) avec une incertitude type \(u(C) = 2 \times 10^{-6}\ \mathrm{mol\cdot L^{-1}}\).
Complément : Un pas vers la terminale - Critère de validité utilisant le calcul d'incertitude (non exigible en classe de première)
Ce point est abordé dans les programmes de terminale et permet de vérifier la compatibilité d'une valeur expérimentale avec une valeur de référence en prenant en compte l'incertitude type calculée. Le critère est le suivant :
si \(\dfrac{\left|C_{expe} - C_{ref}\right| }{u\left(C \right)}<2\) la compatibilité entre la valeur expérimentale et celle de référence est bonne ;
si \(\dfrac{\left|C_{expe} - C_{ref}\right| }{u\left(C \right)}>3\) la compatibilité entre la valeur expérimentale et celle de référence n'est pas bonne ;
Dans le cas de la mesure prise en exemple :
\(\dfrac{\left|C_{expe} - C_{ref}\right| }{u\left(C \right)}=\dfrac{\left|6{,}10\times 10^{-5}-6{,}33\times10^{-5}\right|}{1{,}53\times 10^{-6}}\simeq 1{,}5\)
Ici, on peut donc conclure à la bonne compatibilité entre la valeur expérimentale et la valeur de référence indiquée sur le flacon.

