Exploitation des mesures - L'avancement et le tableau d'avancement
Composition du système chimique à chaque instant
Tableau d'avancement de la réaction
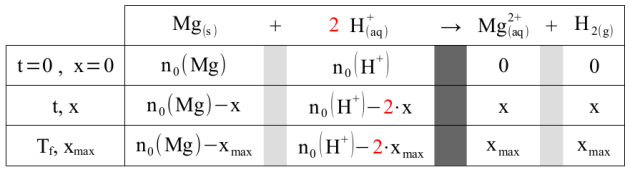
On rappelle ci-dessous le tableau d'avancement de la réaction étudiée.
Les quantités de matière des espèces chimiques présentes à chaque instant dans le système peuvent s'exprimer en fonction des quantités de matière initiales et de l'avancement , en tenant compte des coefficients stœchiométriques de l'équation chimique.
\(n\left(Mg \right) = n_0\left(Mg \right)-x\)
\(n\left(H^+ \right) = n_0\left(H^+ \right)-2 \cdot x\)
\(n\left(Mg^{2+} \right) = x\)
\(n\left(H_2 \right) = x\)
Les quantités de matière initiales étant connues, il suffit d'accéder à la valeur de l'avancement x pour déterminer la composition complète du système chimique.
L'ensemble des mesures exploitées dans ce support correspond à une masse de magnésium introduite \(\mathbf{m(Mg)=0{,}20\ g}\).
Méthode : Accéder à la valeur de l'avancement x
L'avancement x à tout instant n'est accessible que par l'intermédiaire d'une mesure dans le système chimique qui devra être reliée à x par une expression.
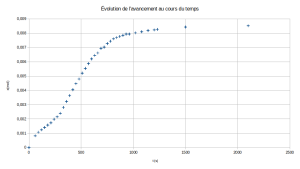
Dans l'activité réalisée en classe, la grandeur mesurée est le volume de dihydrogène dégagé \(V\left(H_2\right)\).
D'après le tableau d'avancement de la réaction, l'avancement x correspond à la quantité de matière de dihydrogène à chaque instant.
\(x=n\left(H_2\right)\)
Ce qui peut s'exprimer en fonction de la grandeur mesurée :
\(x=\dfrac{V\left(H_2\right)}{V_M}\), où VM est le volume molaire des gaz dans les conditions de l'expérience.
En exploitant cette relation dans le tableur, on obtient la représentation graphique ci-contre pour l'avancement de la réaction.
Méthode : Connaître l'évolution des quantités de matière au cours du temps
La connaissance de l'avancement x à chaque instant permet immédiatement d'obtenir les variations des quantités de matière au cours de la réaction en exploitant sur le tableur les relations obtenues par lecture du tableau d'avancement.
\(n\left(Mg \right) = n_0\left(Mg \right)-x\)
\(n\left(H^+ \right) = n_0\left(H^+ \right)-2 \cdot x\)
\(n\left(Mg^{2+} \right) = x\)
\(n\left(H_2 \right) = x\)
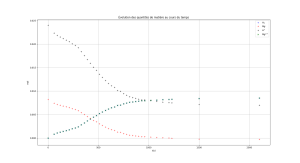
Graphiquement, on constate que le magnésium est le réactif qui est consommé complètement en fin de réaction : on dit que le magnésium est le réactif limitant.
Dans l'état final du système, il reste donc des ions H+. La quantité de matière des ions Mg2+ est confondue sur le graphique avec celle du dihydrogène.
Vous pouvez télécharger le fichier de mesures exploité dans l'exemple précédent.
Critère de fin de réaction - Avancement maximal
Avancement maximal
L'avancement x est une fonction croissante du temps, toujours positive. Elle ne peut cependant pas dépasser une valeur maximale, dépendant des quantités de matière initiales des réactifs : l'avancement maximal xmax.
Définition : Réaction totale
Une réaction chimique est totale si elle évolue jusqu'à la consommation complète d'au moins un de ses réactifs.
Dans ce cas, la valeur de l'avancement en fin de réaction xf est confondue avec celle de l'avancement maximal : \(\mathbf{x_f = x_{max}}\).
Une réaction n'est pas totale si le système chimique n'évolue plus au niveau macroscopique bien que l'avancement maximal ne soit pas atteint : \(\mathbf{x_f < x_{max}}\). C'est le cas des équilibres chimiques où la réaction directe et la réaction inverse entrent en compétition.
Méthode : Détermination de la valeur de l'avancement maximal
La valeur de l'avancement maximal dépend des quantités de matière initiales des réactifs.
La valeur de xmax correspond à la consommation complète d'au moins un des réactifs, donc on peut écrire les relations suivantes :
donc
Cela conduit à plusieurs valeurs possibles de xmax. On retient la plus faible qui correspond à la consommation complète du réactif limitant.
Applications numériques
On conclut donc ici que l'avancement maximal est \(x_{max}=8{,}23\times 10^{-3}\ \mathrm{mol}\) et que le réactif limitant est le magnésium.
Cela correspond à ce qui a été observé dans la plupart des groupes : le magnésium a été complètement consommé.