Exercice : Analyse de l'activité et variations des quantités de matière
Dans cette partie il s'agit de reprendre le cheminement proposé dans la fiche d'activité pour obtenir les variations des quantités de matière des réactifs et produits de la réaction.
Question
Rappel des données et questions de la fiche
Équation bilan de la réaction :
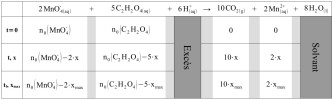
\(\large{2MnO_{4(aq)}^- + 5 C_2 H_2 O_{4(aq)} + 6H^+_{(aq)} \longrightarrow 10 CO_{2(g)}+2Mn^{2+}_{(aq)} + 8 H_2 O_{(l)}}\)
Constitution du système chimique :
\(V_1 = 10{,}0\ \mathrm{mL}\) de solution de permanganate de potassium de concentration apportée \(C_1=1{,}00\times 10^{-3}\ \mathrm{mol\cdot L^{-1}}\) ;\(V_2=10{,}0\ \mathrm{mL}\) de solution d'acide oxalique de concentration apportée \(C_2=1{,}00\times 10^{-2}\ \mathrm{mol\cdot L^{-1}}\) ;
\(V_3=2{,}0\ \mathrm{mL}\) de solution d'acide sulfurique de concentration \(5{,}0\ \mathrm{mol\cdot L^{-1}}\).
Tableau d'avancement et réactif limitant
Justifier qualitativement que les ions H+ sont en large excès et que la quantité de matière du solvant ne présente pas d’intérêt en termes de suivi.
Complétez le tableau d’avancement de la réaction.
Déterminer le réactif limitant de cette réaction ainsi que la valeur de l’avancement maximal xmax.
Suivi de la réaction au cours du temps
Quelle grandeur physique pourrait être facilement mesurée dans le cas présent et être reliée directement à une quantité de matière ?
Effectuez les calculs et opérations nécessaires pour exprimer l’avancement x en fonction de la grandeur mesurée et de quantités de matières initiales.
À partir des données brutes de mesures mises à votre disposition, tracez les représentations graphiques de x, \(n\left(MnO_4^-\right)\), \(n\left(C_2H_2O_4\right)\), \(n\left(Mn^{2+}\right)\) et \(n\left(CO_2 \right)\).
Commenter l’allure des variations de l’avancement x au cours du temps.
Les variations des quantités de matière des réactifs et produits sont-elles en accord avec la valeur de l’avancement maximal et le réactif limitant.
Solution
Tableau d'avancement et réactif limitant
Les ions H+ sont apportés par la solution d'acide sulfurique dont la concentration est beaucoup plus élevée que celles des autres solutions. Les volumes apportés sont eux dans les mêmes ordres de grandeur. Les ions H+ sont donc en très large excès.
Le solvant est l'eau. Les molécules d'eau sont donc présentes elles aussi en très grand nombre dans le système chimique, en très large excès. L'évolution de leur quantité de matière ne présente pas d'intérêt.
Tableau d'avancement complet de la réaction (cliquer pour agrandir) :
Pour déterminer le réactif limitant, on compare les valeurs de \(\dfrac{n_0\left(MnO_4^-\right)}{2}\) et \(\dfrac{n_0\left(C_2H_2O_4\right)}{5}\).
\(\dfrac{n_0\left(MnO_4^-\right)}{2}=\dfrac{C_1 \times V_1}{2}=5{,}00\times 10^{-6}\ \mathrm{mol}\)
\(\dfrac{n_0\left(C_2H_2O_4\right)}{5}=\dfrac{C_2 \times V_2}{5}=2{,}00\times 10^{-5}\ \mathrm{mol}\)
\(\dfrac{n_0\left(MnO_4^-\right)}{2}<\dfrac{n_0\left(C_2H_2O_4\right)}{5}\), donc les ions permanganate sont le réactif limitant.
\(x_{max}=5{,}00\times 10^{-6}\ \mathrm{mol}\)
Solution
Suivi de la réaction au cours du temps
Les ions permanganate sont colorés et leur quantité de matière varie au cours de la réaction. Un suivi spectrophotométrique par mesure de l'absorbance A est donc envisageable.
D'après la loi de Beer-Lambert, on a \(A=k\times \left[MnO_4^-\right]\).
k est déterminé en étalonnant le spectrophotomètre. Avec le matériel utilisé en classe, on a établi que \(k=1500\ \mathrm{L\cdot mol^{-1}}\).
On peut exprimer l'absorbance en fonction de la quantité de matière de permanganate : \(A = k\times \dfrac{n\left(MnO_4^-\right)}{V_{total}}\), avec \(V_{total}=22{,}0\ \mathrm{mL}\).
En utilisant le tableau d'avancement on peut introduire l'avancement de la réaction :
\(A = k\times \dfrac{n_0\left(MnO_4^-\right)-2\times x}{V_{total}}\)
En isolant x, on obtient :
\(x=\dfrac{1}{2}\left(n_0\left( MnO_4^- \right)-\dfrac{A\times V_{total}}{k}\right)\)
On a bien relié l'avancement x à une grandeur physique mesurable. La réaction peut être suivie tout au long de son évolution.
Vous pouvez télécharger la feuille de calcul complétée [ods]. Les représentations graphiques sont dans des onglets différents.
On peut distinguer trois phases dans l'évolution de l'avancement au cours du temps :
en début de réaction l'avancement évolue très peu, la réaction est particulièrement lente ;
lorsque l'avancement augmente de manière significative, il croît de plus en plus rapidement jusqu'à ralentir à nouveau lorsqu'on s'approche de la fin de la réaction ;
en fin de réaction, x atteint un palier et ne varie plus. Le réactif limitant est complètement consommé et x a atteint la valeur de xmax.
Graphiquement, on peut lire la valeur de l'avancement maximal lorsque le palier est atteint : \(x_{max}\simeq5\times 10^{-6}\ \mathrm{mol}\), ce qui est cohérent avec la valeur calculée théoriquement dans la première partie.