Exercice : Niveaux d'énergie d'un atome et radiation lumineuse

Il s'agit dans cet exercice de relier la couleur de la radiation émise à une transition entre deux niveaux d'énergie de l'atome.

Question

On donne les énergies de quelques niveaux de l’atome de mercure sur le diagramme ci-contre.

  1. Déterminer la fréquence \(\mathbf{\nu}\) et la longueur d’onde \(\mathbf{\lambda}\) du photon émis lors de la transition \(E_5 \rightarrow E_4\).

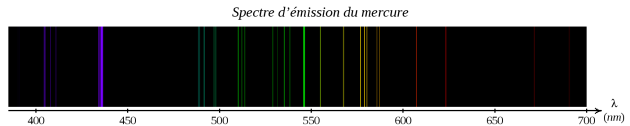
  2. Identifier la raie concernée sur le spectre de l'atome de mercure rappelé ci-dessous.

Quelques niveaux d'énergie de l'atome de mercure.
Spectre d'émission du mercure

Solution

Éléments de correction

  1. on commence par calculer l'écart d'énergie entre ces deux niveaux : \(\Delta E=E_5-E_4\)

    \(\Delta E=-0{,}90+3{,}73=2{,}83\ \mathrm{eV}\)

    La relation de Planck-Einstein utilise les unités du système international, on convertit donc cette énergie en joule :

    \(\Delta E=2{,}83\times 1{,}602\times 10^{-19}\simeq 4{,}53\times 10^{-19}\ \mathrm J\)

    \(\Delta E = E_{photon}=h \cdot \nu = h \cdot \dfrac{c}{\lambda}\)

    donc \(\nu=\dfrac{\Delta E}{h}\) et \(\lambda=\dfrac{h\cdot c}{\Delta E}\)

    Numériquement :

    • \(\nu=\dfrac{4{,}53\times 10^{-19}}{6{,}63\times 10^{-34}}\simeq 6{,}83\times 10^{14}\ \mathrm{Hz}\)

    • \(\lambda=\dfrac{6{,}63\times 10^{-34}\times 3\times 10^8}{4{,}53\times 10^{-19}}\simeq 4{,}39\times 10^{-7}\ \mathrm m \simeq 439\ \mathrm{nm}\)

  2. Cette radiation correspond à la raie violette sur le spectre d'émission de l'atome de mercure.