Exploitation - Arbre de Diane
Observations
On constate :
une coloration progressive en bleu de la solution initialement incolore ;
un dépôt gris sur le fil de cuivre ;
après un temps suffisamment long, une dégradation du fil de cuivre est nettement visible.
Ci-dessous, sa formation en accéléré.
Réaction chimique mise en jeu
Compte tenu des éléments chimiques présents dans l'état initial du système, on tire des observations précédentes les conclusions suivantes :
le dépôt gris observé est de l'argent solide : Ag ;
la coloration bleue de la solution est due à la formation d'ions cuivre II : Cu2+.
On peut donc en déduire que :
le cuivre solide Cu forme des ions Cu2+ ;
les ions argent Ag+ forment de l'argent solide Ag.
D'où l'équation de la réaction chimique équilibrée de façon à conserver les éléments chimiques et la charge électrique :
Tableau d'avancement de la réaction et exploitation quantitative
Tableau d'avancement de la réaction
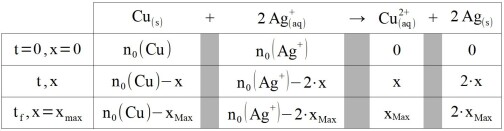
État initial du système (exemples de valeurs)
Quantité de matière de cuivre : \(n_0 \left(Cu\right)=\dfrac{m_0 \left(Cu \right)}{M\left(Cu\right)}\)
Masse du fil de cuivre : \(m_0\left(Cu\right)=2{,}14\ \mathrm g\)
Donc \(n_0 \left(Cu\right)=\dfrac{2{,}14}{63{,}5}\simeq 3{,}37\times 10^{-2}\ \mathrm{mol}\)
Quantité de matière d'ions argent : \(n_0\left(Ag^+\right)=C\left(AgNO_3 \right)\times V\left(AgNO_3 \right)\)
Volume de solution introduit : \(V\left(AgNO_3 \right)=15{,}0\ \mathrm{mL}\).
Concentration molaire de la solution : \(C\left(AgNO_3 \right)=0{,}1\ \mathrm{mol\cdot L^{-1}}\)
Donc \(n_0\left(Ag^+\right)=0{,}1\times 15{,}0\times 10^{-3}\simeq 1{,}50\times 10^{-3}\ \mathrm{mol}\).
Avancement maximal et réactif limitant
Si le cuivre est le réactif limitant : \(x_{max}=n_0\left(Cu \right)=3{,}37\times 10^{-2}\ \mathrm{mol}\).
Si les ions argent sont le réactif limitant : \(x_{max}=\dfrac{n_0\left(Ag^+\right)}{2}\simeq 7{,}50\times 10^{-4}\ \mathrm{mol}\)
\(\dfrac{n_0\left(Ag^+\right)}{2}<n_0\left(Cu \right)\), donc le réactif limitant est constitué des ions argent Ag+ et \(x_{max}\simeq 7{,}50\times 10^{-4}\ \mathrm{mol}\)
Perte de masse du fil de cuivre
D'après le tableau d'avancement, la quantité de matière de cuivre diminue de la valeur de xmax.
Cela correspond à une quantité de matière perdue \(\Delta n\left(Cu\right)=x_{max}=7{,}50\times 10^{-4}\ \mathrm{mol}\)
Soit une variation de masse \(\Delta m\left(Cu \right)=\Delta n\left(Cu\right)\times M\left(Cu\right)\).
Application numérique :
\(\Delta m\left(Cu \right)=7{,}50\times 10^{-4}\times 63{,}5\simeq 4{,}76\times 10^{-2}\ \mathrm g\)
On peut vérifier expérimentalement ce résultat en pesant le fil de cuivre avant et après réaction.
Les mesures effectuées en classe ont confirmé les calculs théoriques.
Masse d'argent formé
D'après le tableau d'avancement, la quantité de matière formée est égale à \(2 \cdot x_{max}\), \(1{,}50\times 10^{-3}\ \mathrm{mol}\)
Masse molaire de l'argent : \(M\left(Ag\right)=107{,}9\ \mathrm{g \cdot mol^{-1}}\)
Masse d'argent formée : \(m_f\left(Ag\right)=1{,}50\times 10^{-3}\times 107{,}9\simeq 0{,}16\ \mathrm g\)
La vérification expérimentale de cette masse formée est plus délicate car il est nécessaire de sécher l'argent formé.
