Exercice : Activité expérimentale - Mesure de la célérité d'ondes mécaniques dans différents contextes
Il s'agit d'aborder la notion de célérité d'une onde à travers différentes mesures et d'étudier quelques facteurs pouvant l'influencer.
Le logiciel utilisé ici (Pymécavidéo) pour les pointages sur les vidéos est téléchargeable en vous rendant à la section Quelques logiciels exploités dans le cours de physique-chimie.
Question
Vous pouvez télécharger ci-dessous la fiche d'activité.
Solution
1. Onde le long d'une corde
Vous pouvez consulter les résultats des pointages des positions du front d'onde dans le document en téléchargement ci-dessous. Ils peuvent différer légèrement de vos propres résultats.
On a les deux résultats suivants :
pour la corde non tendue : \(v \simeq 10{,}7\ \mathrm{m \cdot s^{-1}}\) ;
pour la corde tendue : \(v \simeq 18{,}3\ \mathrm{m \cdot s^{-1}}\).
On constate expérimentalement que la tension de la corde a une influence la vitesse de propagation de l'onde : plus la corde est tendue, plus la célérité de l'onde augmente.
La célérité v de l'onde s'exprime en fonction de la tension T : \(v=\sqrt {\dfrac{T}{\mu}}\).
Cette expression est bien cohérente avec l'observation expérimentale :
si la tension T augmente, le rapport \(\dfrac{T}{\mu}\) augmente aussi ;
la fonction racine carrée étant croissante, la valeur de la vitesse v augmente donc.
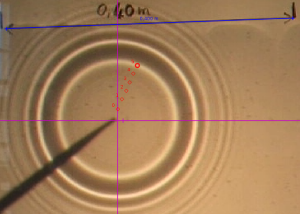
2. Onde circulaire à la surface de l'eau
On repère les positions du front d'onde dans le cas d'une vaguelette créée à la surface d'une cuve à onde.
L'origine étant placée au point de chute de la goutte, on détermine dans une feuille de calcul le rayon du front d'onde circulaire à partir des coordonnées x et y.
Vous pouvez télécharger ci-dessous un exemple de résultats issus d'un pointage.
Expérimentalement, on obtient la valeur de la vitesse ci-dessous :
\(v\simeq0{,}386\ \mathrm{m \cdot s^{-1}}\)
On peut utiliser la valeur de la vitesse pour estimer la profondeur de la cuve à l'aide de la relation \(v=\sqrt{g \times h}\).
On a donc : \(h=\dfrac{v^2}{g}\).
Numériquement :
\(h=\dfrac{0{,}386^2}{9{,}81}\simeq0{,}015\ \mathrm m \simeq 1{,}5\ \mathrm{cm}\).
La profondeur de la cuve obtenue est cohérente avec la géométrie de la cuve à ondes utilisée en classe.
3. Détermination de la vitesse du son dans l'air - Éléments de correction sur la partie incertitudes
On reprend ici un calcul d'incertitude sur la mesure de la vitesse du son à partir d'un résultat obtenu lors de la séance.
L'estimation de l'incertitude est une étape essentielle dans la présentation d'un résultat de mesure, car elle permet d'exprimer le résultat avec un nombre de chiffres significatifs cohérent et de tester, le cas échéant, sa compatibilité avec une valeur de référence.
Récapitulatif de la mesure :
distance entre les deux micros : \(d=3{,}915\ \mathrm m\) ;
décalage temporel entre les deux chronomètres : \(\Delta t=0{,}023\ \mathrm s\) ;
vitesse du son obtenue : \(v_{son}=\dfrac{2\cdot d}{\Delta t}\simeq340{,}43\ \mathrm{m \cdot s^{-1}}\).
Remarque : le nombre de chiffres significatifs sera ajusté en fonction du résultat du calcul d'incertitude.
Estimation de l'incertitude
Grandeur | Valeur / précision | Expression de l'incertitude | Valeur de l'incertitude |
|---|---|---|---|
\(\mathbf d\) | \(d=3{,}915\ \mathrm m\) \(p = 0{,}001\ \mathrm m\) | \(u\left(d\right)=\dfrac{p}{\sqrt 6}\) | \(u\left(d\right)=4{,}08\cdot10^{-4}\ \mathrm m\) |
\(\mathbf{\Delta t}\) | \(\Delta t=0{,}023\ \mathrm s\) \(p = 0{,}001\ \mathrm s\) | \(u \left(\Delta t \right)=\dfrac{p}{2\cdot \sqrt 3}\) | \(u \left(\Delta t \right)=2{,}89\cdot 10^{-4}\ \mathrm s\) |
\(\mathbf{\dfrac{u\left(v_{son}\right)}{v_{son}}}\) | \(v_{son}\simeq340{,}43\ \mathrm{m \cdot s^{-1}}\) | \(\dfrac{u\left(v_{son}\right)}{v_{son}}=\sqrt{\left(\dfrac{u(d)}{d} \right)^2+\left(\dfrac{u(\Delta t)}{\Delta t} \right)^2}\) | \(\dfrac{u\left(v_{son}\right)}{v_{son}}=0{,}0126\) |
\(\mathbf{u\left(v_{son}\right)}\) | \(u\left(v_{son}\right)\) : obtenue en multipliant l'incertitude relative par la valeur de vson. | \(4{,}28\ \mathrm {m \cdot s^{-1}}\) |
Écriture du résultat final
Pour écrire le résultat final :
on arrondit l'incertitude-type à un seul chiffre significatif ;
on écrit le résultat avec la même précision que l'incertitude-type.
Ici \(u\left(v_{son}\right)\simeq4\ \mathrm{m \cdot s^{-1}}\)
L'incertitude-type porte donc sur le chiffre des unités. On écrit le résultat de la mesure en arrondissant à l'unité, les chiffres significatifs suivants n'ont pas de sens au vu de la précision de notre mesure.
On peut annoncer le résultat de la mesure de la façon suivante :
La vitesse du son mesurée est \(v_{son}=340\ \mathrm{m \cdot s^{-1}}\) avec une incertitude type \(u\left(v_{son} \right)=4\ \mathrm{m \cdot s^{-1}}\)
Remarque :
Lors de vos mesures, vous avez pu constater que la dispersion des résultats est très grande et qu'une élimination des résultats aberrants est nécessaire avant de mener les calculs à leur terme.