Objectifs et pré-requis⚓
Objectifs
aborder la notion de période et de fréquence d'un son ;
les associer à la sensation sonore ;
enregistrer un son à l'aide d'une application mobile ;
effectuer les mesures permettant de déterminer avec la plus grande précision possible la période et la fréquence du son.
Pré-requis
Il faut disposer de l'application mobile gratuite Phyphox ![]() téléchargeable pour :
téléchargeable pour :
Phyphox permet d'utiliser l'ensemble des capteurs du téléphone pour faire des mesures en physique.
Même si nous n'utiliserons pas cette fonctionnalité ici, les données sont exportables pour être traitées dans un tableur ou dans tout autre logiciel.

Méthode : Enregistrer un son avec Phyphox et mesurer une période
Ci-dessous la procédure pour enregistrer un signal sonore avec l'application Phyphox et en déterminer la période en utilisant l'outil de mesure de l'application.
Définitions et rappels⚓
Définition : Phénomène périodique
Un phénomène est dit périodique s'il se reproduit identique à lui-même à intervalles de temps réguliers.
La période du phénomène est la durée minimale séparant deux états strictement identiques du système.
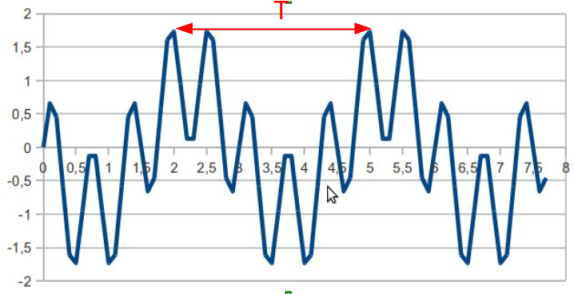
Sur un signal, le caractère périodique se manifeste par la répétition d'un même motif au cours du temps. La durée de ce "motif de base" est appelée la période du signal. Elle est le plus souvent notée T et s'exprime en seconde (s).
Sur le signal ci-contre, on a repéré :
surligné en rouge, une partie du signal qui se répète régulièrement au cours du temps ;
la période T du signal par la double flèche rouge ;
l'amplitude A du signal.
Définition : Fréquence d'un phénomène périodique
Par définition, la fréquence f d'un phénomène périodique correspond au nombre de répétitions par seconde.
La fréquence s'exprime en hertz (Hz).
Mathématiquement, période et fréquence sont liées par :
Manipuler période et fréquence
Question⚓
Les quelques questions ci-dessous vous permettent de vérifier que :
vous savez repérer un signal périodique ;
vous savez repérer une période sur l'enregistrement d'un signal ;
vous savez manipuler la relation mathématique entre période et fréquence.
Question 1
Identifier les signaux périodiques parmi les signaux ci-dessous et justifier à chaque fois en une phrase simple.



Question 2
Sur le signal ci-contre :
Déterminer graphiquement la période T.
En déduire par un calcul la fréquence f, exprimée en hertz (Hz).
Question 3
La période de révolution de la Terre sur son axe est \(T=24\ \mathrm h\).
Calculer la fréquence f de ce mouvement et l'exprimer en Hz.
Question 4
La fréquence de rotation d'un tambour de machine à laver est \(f=1400\ \mathrm{tr \cdot min^{-1}}\) (tours par minute).
Calculer la période T de ce mouvement et l'exprimer en s.
Solution⚓
Question 1
Le signal n°1 montre un motif qui se répète régulièrement, il est donc périodique.
Le signal n°2 est irrégulier, ses variations ne font apparaître aucune répétition. Il n'est pas périodique.
Le signal n°3 montre des maxima et minima régulièrement espacés, mais son amplitude diminue au cours du temps. Il n'est donc pas périodique.
Question 2
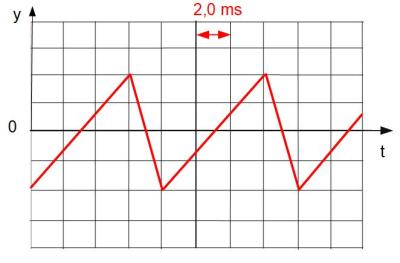
La période du signal peut se mesurer comme indiqué ci-contre.
Graphiquement, la période correspond à quatre divisions, chacune correspondant à une durée \(\tau=2{,}0\ \mathrm {ms}\).
On a donc \(T=4 \times \tau = 8{,}0\ \mathrm {ms}\).
La fréquence se calcule à partir de la période par la relation \(f=\dfrac{1}{T}\), en exprimant la période en seconde.
\(f=\dfrac{1}{8{,}0 \times 10^{-3}} =125\ \mathrm {Hz}\)

Question 3
Avant de calculer la fréquence, il faut exprimer la période T en seconde.
\(T=24\ \mathrm h = 24 \times 3600=86400\ \mathrm s\)
La fréquence de ce mouvement est donc :
\(f = \dfrac{1}{86400}\simeq 1{,}16 \times 10^{-5}\ \mathrm{Hz}\)
Question 4
Avant de calculer la période T en seconde, il faut convertir la fréquence en hertz, donc en tours/seconde.
\(1\ \mathrm{min} = 60\ \mathrm s\)
\(f=\dfrac{1400}{60} \simeq 23{,}3\ \mathrm {Hz}\)
On a donc :
\(T=\dfrac{1}{23{,}3} \simeq 4{,}29 \times 10^{-2}\ \mathrm s\)
Enregistrement et analyse de notes de musiques⚓
Question⚓
On donne dans le tableau ci-dessous les fréquences de quelques notes de musique.
Note | Do3 | Ré3 | Mi3 | Fa3 | Sol3 | La3 | Si3 |
|---|---|---|---|---|---|---|---|
f (Hz) | 262 | 294 | 330 | 349 | 392 | 440 | 494 |
Vous joindrez à chacune de vos réponses (devoir de l'ENT, mail ou Pronote) une capture d'écran (voir exemple) montrant la fenêtre de mesures justifiant votre valeur de la période T. Utilisez la fonction de capture d'écran de votre téléphone (combinaison de touches) et non celle intégrée à Phyphox qui ne capture pas la fenêtre de mesures.
Question 1 - Identifier une note
On cherche à déterminer la note jouée par cet instrument.
En vous référant à la méthode présentée dans les pré-requis, utilisez Phyphox pour déterminer la période et la fréquence de cette note.
Identifier la note jouée en vous référant au tableau fourni. Justifiez en explicitant vos calculs et mesures (capture d'écran et raisonnement).
Question 2 - Influence de la fréquence
On donne deux notes de fréquences différentes, jouées par le même instrument.
Déterminez les fréquences f1 et f2 des notes n°1 et n°2 à l'aide de l'application Phyphox comme indiqué dans le tutoriel vidéo.
Comparez ces deux fréquences en calculant le rapport \(\dfrac{f_1}{f_2}\).
Quel lien y a-t-il entre la fréquence d'une note et la perception sonore ?
Question 3 - Sauriez-vous chanter un la ?
On donne ci-dessous les fréquences de trois la.
Note | La2 | La3 | La4 |
|---|---|---|---|
f (Hz) | 220 | 440 | 880 |
T (s) | |||
T (ms) |
Objectif : vous devez produire un la, chanté ou sifflé, le plus juste possible. Vous choisirez une des trois notes ci-dessous en fonction de votre tessiture.
Reproduisez au brouillon le tableau ci-dessus et effectuez les calculs des périodes en s, puis en ms.
Enregistrez votre la chanté avec l'application Phyphox et vérifiez que la période du signal correspond à ce que vous avez calculé dans le tableau.
Joignez à votre réponse, dans l'ENT ou par mail, une capture d'écran de Phyphox montrant la fenêtre de mesure (voir exemple) afin de justifier que vous avez bien chanté un la. Utilisez les fonctions de capture d'écran de votre téléphone et non celle intégrée à Phyphox qui ne capture pas la fenêtre de mesures.
Solution⚓
Question 1 - Identifier une note
À l'aide de l'application Phyphox, on enregistre le son et on mesure sa période T.
On obtient : \(T \simeq 3{,}77\ \mathrm {ms} \simeq 3{,}77 \times 10^{-3}\ \mathrm s\)
La relation entre période et fréquence permet de calculer la fréquence de la note enregistrée :
\(f=\dfrac{1}{T}\)
Soit numériquement :
\(f = \dfrac{1}{3{,}77 \times 10^{-3}} \simeq 265 \ \mathrm {Hz}\)
On détermine expérimentalement une fréquence de \(\mathbf{265\ Hz}\) pour la note jouée. D'après le tableau de correspondance des fréquences et notes on en déduite que la clarinette joue un Do3.
Question 2 - Influence de la fréquence
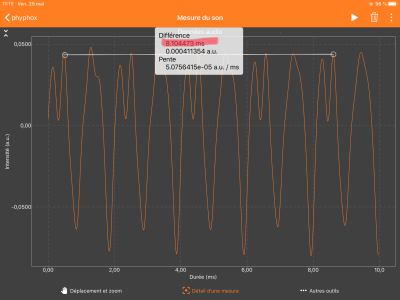
Les illustrations ci-contre montrent les mesures des périodes des deux notes à l'aide de Phyphox.
Note n°1 : \(4 \times T_1\simeq 8{,}10 \times 10^{-3}\ \mathrm s\)
soit \(T_1 = \dfrac{8{,}10 \times 10^{-3}}{4} \simeq 2{,}025 \times 10^{-3}\ \mathrm s\)
Donc : \(f_1 = \dfrac{1}{T_1} = \dfrac{1}{2{,}025\times 10^{-3}} \simeq 494\ \mathrm{Hz}\)
Note n°2 : \(3 \times T_2\simeq 8{,}54 \times 10^{-3}\ \mathrm s\)
soit \(T_2 = \dfrac{8{,}54 \times 10^{-3}}{3} \simeq 2{,}847 \times 10^{-3}\ \mathrm s\)
Donc : \(f_2 = \dfrac{1}{T_2} = \dfrac{1}{2{,}847\times 10^{-3}} \simeq351 \ \mathrm{Hz}\)
On a :
\(\dfrac{f_1}{f_2}=\dfrac{494}{351} \simeq 1{,}4\).
La note n°1 a une fréquence 1,4 fois plus élevée que la note n°2. Du point de vue de la perception sonore, la note n°1 est plus aiguë que la note n°2.
La fréquence est détermine la hauteur du son, c'est-à-dire son caractère plus ou moins grave ou aigu. Plus la fréquence est élevée, plus le son est aigu.
Question 3 - Sauriez-vous chanter un La ?
1. On calcule la période à l'aide de la relation \(f=\dfrac{1}{T}\).
Note | La2 | La3 | La4 |
|---|---|---|---|
f (Hz) | 220 | 440 | 880 |
T (s) | \(4{,}55\times 10^{-3}\ \mathrm s\) | \(2{,}27 \times 10^{-3}\ \mathrm s\) | \(1{,}14 \times 10^{-3}\ \mathrm s\) |
T (ms) | 4,55 | 2,27 | 1,14 |
2. Ci-contre, un enregistrement qui montre une note dont la période est très proche de celle d'un La2.
\(T_{\text{La2}}=4{,}55\ \mathrm {ms}\)
\(T_\text{note}\simeq 4{,}54\ \mathrm {ms}\)