Calculer les modèles simples avec la fonction polyfit
polyfit est une fonction de la bibliothèque numpy qui permet, comme son nom l'indique, d'obtenir les paramètres de modélisations polynomiales. Elle est d'une utilisation plus simple que curve_fit.
Méthode : Utilisation de la fonction
On commence par importer la bibliothèque numpy.
import numpy as np
On suppose qu'on dispose de deux listes :
les données en abscisses : X ;
les données en ordonnées : Y.
On utilise polyfit comme indiqué ci-dessous si on souhaite une modélisation de degré 2 du type \(Y = a \cdot X^2 + b\cdot X +c\).
coefficients = np.polyfit(X, Y, 2)
coefficients est une liste telle que dans notre exemple :
coefficients[0] est le paramètre a ;
coefficients[1] est le paramètre b ;
coefficients[2] est le paramètre c ;
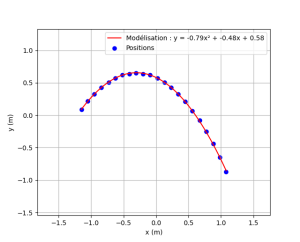
Exemple : Obtention de l'équation d'une trajectoire dans le cas d'un mouvement parabolique
On suppose qu'on a effectué un pointage sur le lancé d'une balle de golf.
On dispose des listes des abscisses et des ordonnées.
On souhaite placer sur le même graphique :
les positions pointées ;
la trajectoire modélisée avec son équation.
Le programme ci-dessous exploite la fonction polyfit pour obtenir l'équation de la trajectoire et tracer les représentations souhaitées.
"""Ce programme illustre l'utilisation de polyfit pour obtenir l'équation d'une trajectoireà partir de positions issues d'un pointage sur une vidéo"""import matplotlib.pyplot as plt # Importation de la bibliothèque graphique
import numpy as np # Importation de numpy pour utiliser la fonction polyfit
"""Ci-dessous : saisies des listes des abscisses et des ordonnées issues de pointages"""x = [-1.15, -1.05, -0.95, -0.84, -0.73, -0.63, -0.52, -0.41, -0.31, -0.20, -0.09, 0.02, 0.13, 0.23, 0.34, 0.45, 0.56, 0.67, 0.77, 0.88, 0.98, 1.08]
y = [0.09, 0.22, 0.33, 0.43, 0.51, 0.57, 0.62, 0.64, 0.65, 0.64, 0.62, 0.57, 0.51, 0.43, 0.33, 0.21, 0.07, -0.08, -0.25, -0.44, -0.65, -0.87]
"""Utilisation de la fonction polyfit pour déterminer les paramètres de la modélisation parabolique de latrajectoire : y = a.x² + b.x + c"""coefficients = np.polyfit(x, y, 2) # Les arguments de polyfit sont la liste en abscisses, la liste en ordonnées et le degré du polynôme
"""Calcul du modèle pour 100 valeurs prises entre xmin et xmax"""xmod = np.linspace(min(x), max(x), 100)
modele = [coefficients[2] + coefficients[1] * val + coefficients[0] * val**2 for val in xmod] # Calcul du modèle
"""On place sur un même graphique les pointages et la trajectoire modélisée"""plt.figure(1)
plt.scatter(x, y, marker = "o", color = "blue", label = "Positions")
plt.plot(xmod, modele, color = "red", label = f"Modélisation : y = {coefficients[0]:.2f}x² + {coefficients[1]:.2f}x + {coefficients[2]:.2f}") # L'étiquette (label) utilise les f-string pour la mise en forme
plt.xlabel("x (m)")
plt.ylabel("y (m)")
plt.legend() # Affichage de la légende
plt.show() # Affichage du graphique